Calcolare l’area compresa tra due funzioni

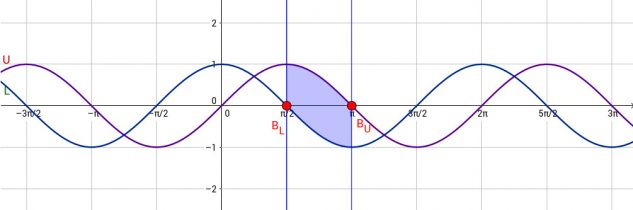
Per calcolare l’area della parte di piano racchiusa tra due funzioni di equazioni assegnate, è in primo luogo necessario determinare (qualora non siano dichiarati esplicitamente) gli estremi orizzontali a e b di tale superficie. Se la richiesta è relativa all’area della sezione chiusa e limitata formata dalle due funzioni stesse, tali estremi coincideranno con le soluzioni del sistema { y=f(x), y=g(x) }, ovvero eguagliando i termini:

f(x) – g(x) = 0

A questo punto, per determinare l’area sarà sufficiente calcolare l’integrale tra a e b di |f(x) – g(x)|. Questo procedimento è indubbiamente il più veloce, e la presenza del valore assoluto evita qualsiasi problematica relativa a quale delle due funzioni si trovi nella parte superiore/inferiore del grafico.

Naturalmente il calcolo dell’area compresa tra una generica funzione e l’asse x equivale alla risoluzione dell’integrale tra a e b di |f(x) – 0|, ovvero l’integrale del valore assoluto della funzione stessa.